We start with our sun as an example:
| Energy source of our solar system | |
| Sun is a typical star -> good example for all other stars |
The material for the many stars needs to be organized.
1. Luminosity, Distance, Size
First and most obvious parameter: How bright is the star in the sky?
| old classification | according to sensitivity of the eye | ||
| Bright 1 ..... 2 ...... 3 ...... 5 ...... 6 Faint | |||
| (higher value of magnitude means fainter) | |||
| Brighter can mean | -> more luminous | and/or |
| -> closer to us | Ergo: We need the Distance! |
| Sun: | r = 150 Mio km |
| derived through Kepler's 3rd law and parallax to other planets | |
| Stars: | parallax with the orbit of the Earth as baseline |
| (largest baseline possible) | |
| very skinny triangle (works up to approx. 100 parsec) |
| Sun: | d = 1.39 Mio km | derived from angular size (skinny triangle) | |
| Stars appear as points, even in largest telescopes | |||
Energy flux (sun): L = 4*1026 Watt
derived from energy flowing through 1 m2 at the distance of the Earth
| approx. 1400 Watt/m2 (solar constant) | |||
| and multiplied by the surface of the sphere at the distance of the Earth | |||
Total energy radiated on Earth is > 10000 times the energy used by mankind!!
| -> may be enough for our energy demands |
Our energy usage must remain at tiny fraction of the solar energy flux!
| Artificial production of only 1.3% of the solar energy flux | |
| -> 1o C temperature increase on Earth | |
| radiation balance (as discussed for sun below) |
| Stars: | L = | total energy emitted by the star | |
| (derived from magnitude and distance: parallax). | |||
Magnitude (or Brightness) scales like Luminosity*1/Distance2
2. Spectroscopic Measurements
| Sun: | T = 5500 K | derived from solar radiation | |
| sun is the best "black body" in the solar system | |||
| --> photons have many collisions with matter before escaping | |||
| --> photons "know" about temperature | |||
| Black Bodies: | stars, planets, cloud tops, rocks in rings, dust particles | ||
| Not Black Bodies: | corona, nebulae (not dense) | ||
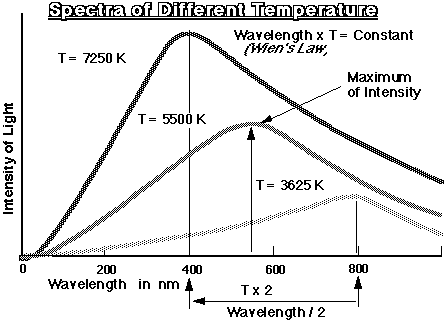
A "Blackbody" spectrum
| a) is peaked with a distinct maximum at a certain wavelength | |
| b) Its total radiation and distribution over wavelength depends only on T |
| a) Wien's Law: | |||
| temperature* wavelength(max) = constant | |||
| sun has maximum at green (our eyes work best for this color) -> T | |||
| hot stars: | blue, UV. | ||
| sun: | yellow. | ||
| cool stars: | red. | ||
| very cool stars: | |||
| protostars: | |||
| dust heated by stars: | IR. | ||
| planets: | |||
| cloudtops: | |||
-> We can get the temperature from the color or the wavelength with the maximum

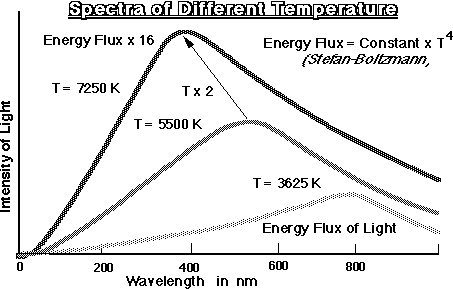
| b) Stefan Boltzmann Law: | ||
| energy flux = constant * T4 | ||
| in words: higher energy flux | -> means higher temperature of the star | |
| or a brighter star surface |
Application to the observation of stars:
| From distance and magnitude combined | ->Luminosity | ||
| From Wien's Law | -> Temperature | ||
| Form Stefan-Boltzmann Law | -> Energy Flux/area | ||
| Combine Luminosity and Energy Flux/Area | -> Surface of Star | ||
| -> Diameter | |||
| Sun: | 75% H, 23% He, 2% "metals" |
| Derived from Fraunhofer lines in spectrum | |
| Each atom, ion, molecule absorbs or emits at its own set of frequencies. | |
| Reason: | Electrons are confined to specific orbits in atoms |
| (Bohr's Model of atoms <-> Quantum Mechanics) |
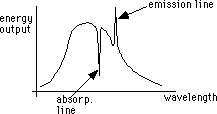
| Absorption line: | material in front of "black body" | -> sun's atmosphere |
| Emission line: | thin material radiating | -> outer atmosphere |
| -> identify |
Nebulae = gas clouds = emission lines (not black body)
Galaxies = sum of black bodies from many stars (plus the stars' absorption lines)
Uses (for all stars):
| a) What's there? (H, He, etc.). | determined by specific set of lines | |||
| Hydrogen alpha line = red | (most abundant element) | |||
| (Hydrogen at 10,000K or near a star at 10,000K) | ||||
| e.g. | ||||
| chromosphere | ||||
| prominences | -> red is the color of the universe! | |||
| nebulae | ||||
| b) Abundances: | relative intensity of lines |
| -> differences in composition |
| The universe was born with H and He only (almost) | ||
| Population I: 75% H, 23% He, 2% heavy elements ("recycled" material ) | Sun is Population I | |
| Population II: 77% H, 23% He, few heavy elements ("more primitive" material) | ||
| Where are the true "Þrst" stars (H, He only)? |
3. Stellar Mass and Density
| M = 2*1030 kg | derived from Kepler's 3rd law (planets) |
B) Binary Stars and Mass Determination
Velocities can be measured with Doppler Effect:
| Spectral lines key to Doppler: | (we know the frequencies when there is no motion) | |||
| Velocity Away from us | --> | frequency decreases | = redshift | |
| Velocity Toward us | --> | frequency increases | = blueshift | |
| Velocity Across | --> | no shift |
2 possible ways to get the star mass:
| 1) Doppler effect | -> Velocity of stars | |
| + orbital period | ||
| or | ||
| 2) Distance of binary stars | -> distance between 2 stars | |
| + orbital period | ||
| use Kepler's 3rd law | -> mass of stars |
| Sun: | r = 1.4 g/cm3 | combined from 2B) and 3A) |
| 1.4 times density of water | ||
| Red Giants: | much less dense | |
| White Dwarfs: | much denser | |
Determination of the Star Parameters
| Parameter | Observation | Deduction |
| Apparent Magnitude | Measure Brightness | ||
| Distance | Parallax | Distance | |
| Luminosity | Combine: | ||
| Distance and Apparent Magnitude | |||
| Surface Temperature | Color of Star (Wien's Law) | ||
| Spectral Lines | |||
| Energy Flux/Area | from Temperature | ||
| (Stefan-Boltzmann) | |||
| Size | Combine: Luminosity | ||
| Energy Flux/Area | |||
| Composition | Spectral Lines | Elements | |
| Mass | Distance or Velocity and | Use Kepler's 3d Law | |
| Orbital Period of Binary Stars | |||
According to their color stars have been organized in classes:
Essentially luminosity vs. temperature.
Main sequence (distinct line filled with stars through the center diagonal)
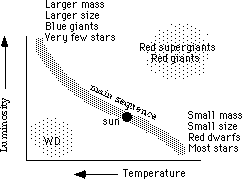
a) Sizes: White Dwarfs hot (high energy flux density) and dim -> small
b) Spectral Parallax:
c) Variable stars (e.g. Cepheids)
Luminosity of stars varies like Mass * Mass * Mass * Mass
The poor are saving and the rich are squandering -> massive stars die faster
Determination of Star Distances
| Method | Observations How to do? |
| (Range) |
| Geometric Parallax | Measure star position Use diameter of Earth's orbit |
| (6 months apart as baseline!) | |
| (approx. 100 Parsec) | -> angle and Earth's orbit lead to distance |
| (like distance of the moon or planets) |
| Spectroscopic Parallax | Measure temperature Find position of star in HR |
| of star diagram | |
| -> get luminosity and apparent magnitude | |
| (approx. 20,000 Parsec) | -> luminosity and magnitude lead to distance |
| Cepheid Variables | Measure period Period determines of variable luminosity |
| and apparent magnitude | |
| (approx. 20 million Parsec) | -> luminosity and magnitude lead to distance |