
Performs physical experiments
| with falling bodies and balls rolling down a track | |
| concludes that velocity increases (or decreases) under action of force |
| 1st Law) | Without any forces an object remains in its natural state: |
| rest or constant straight motion |
| 2nd Law) | A force accelerates an object with the mass as multiplicative constant | ||
| Force = Mass * Acceleration | F = m * a | ||
| 3rd Law) | Interaction of two objects | |
| Action on one | -> equal and opposite Re-action on the other | |
| Force = Counterforce | ||
B) Universal law of gravitation:
a) Universal force on all bodies on Earth
| objects | -> falling to ground | by gravity |
Concludes that: acts also at distance from Earth
| moon | -> falling towards Earth by gravity |
| -> gravity bends natural straight path into circle |
Note: Force is necessary to constantly change the natural straight path into a circle!!
| centripetal force (pulling toward center) = gravitational force | |||
| is balanced by centrifugal (pseudo)-force of motion | |||
b) Force decreases with distance
| Force spread over surface area | > decreases with square of the distance |
c) Involves masses
| Center mass pulls: | > force proportional to mass in center |
| Mutual attraction (Newton's third law! ) | > both masses in formula |
Force = G*Mass1*Mass2/Distance2

d) Explains:
Kepler's 3 Laws
i) Kepler's 1st Law Ellipses found as natural orbits in gravitation
ii) Conservation of energy
Kinetic energy + gravitational energy = constant (for each planet separately)
Gravitational energy increases with distance from sun ->
Kinetic energy (i.e. Velocity) of each planet decreases
as it gets further from sun
iii) Conservation of angular momentum (analogy: ice scater performing pirouette)
Angular momentum = constant (for each planet separately).
ii + iii) -> Kepler's 2nd Law Equal areas
These conservation laws apply also to moons orbiting planets.
iv) Provides interpretation for the Constant in Kepler's 3rd Law:
For small bodies orbiting a heavy central object (planets around sun or star)
[M in solar masses] * (period in years)2 = (average distance in AU)3
But: Mutual attraction revises Kepler's 3rd Law: (Use the sum of all masses!)
[(m1 + m2) in solar masses] * (period in years)2 = (average distance in AU)3
or for circular orbits:
(m1 + m2) = (1/G)(velocity1 + velocity2)2 * (distance)
For example: Earth speeds with about 30 km/sec at 1 AU
Note: Large velocities require large masses to keep things from flying apart!
Spinoffs: predicted return of Halley's comet
| Astronomy | --> spawned new physical laws |
But: With what to compare? or which are our weigths for the celestial scale?
a) Weigh Earth first -> get G (gravitational constant!)
Compare gravitational pull of known Mass with pull of Earth
Mearth = 6 . 1024 kg
b) Deduce other masses from:
| Orbits of | --> | m1 + m2. | ||
| Moons | --> | Planet's mass | 1.9 . 1027 kg (Jupiter) | |
| Planets | --> | Sun's mass | 2 . 1030 kg | |
| Binary stars | --> | Stars' masses | 0.1 - 60 Msun | |
| Stars in a cluster | --> | Cluster's mass | 100 - 100,000 Msun | |
| Stars in a galaxy | --> | Galaxy's mass | 107 - 1012 Msun | |
| Galaxies in a cluster | --> | Cluster's mass | 1012 - 1015 Msun |
-> Outlook: "Missing Mass Problem" or "Dark Matter Problem":
Masses of galaxies and clusters determined from gravity are
much larger than the masses we "see" in the universe
a) Small deflections of planet/spacecraft trajectories
| --> masses (of planets, moons; Halley's comet) from mutual attraction | ||||||
| Example: | Deviation of Uranus' orbit | -> Discovery of Neptune (1846) | ||||
| Spinoff: | fancy math (Calculus, 19th century) still used today | |||||
b) If a visible star etc. wiggles -> it has a companion
| Star's position wiggles | Þ astrometric binary Þ discovery of White Dwarfs | ||
| modern method to find "planet" around star (51 Pegasi) | |||
| Star's velocity wiggles (Doppler) | --> spectroscopic binary | ||
| modern method to find "planet" around a pulsar | |||
| Spacecraft trajectories: | ||||||||
| Voyagers, Galileo, Ulysses, Solar Probe used gravity | ||||||||
| to change the energy (works because the planets are | ||||||||
| moving) and angular momentum of the spacecraft. | ||||||||
| Ulysses used gravity to "tip" the angular momentum of the spacecraft. | ||||||||
| Natural examples: | |||||||
| Periodic comets with apogee near Jupiter | |||||||
| their orbit was changed by a near encounter with Jupiter | |||||||
| Capture of comets into orbit around Jupiter (moon assist) | |||||||
| collision with Jupiter (Shoemaker - Levy) | |||||||
A) Mutual attraction -> combined rotation about gravity center
MEarth ~ 80 * MMoon
-> center of combined rotation = center of gravity inside Earth
a) Daily tides:
| 2 high tides and 2 low tides per day | ||||
| Due to: | 1/(distance)2 dependence of gravity and combined rotation | |||
| on the side of the moon | gravity creates bulge | |||
| on the opposite side | centrifugal force creates the bulge | |||

| Tidal day = solar day + 50 minutes (approximately). | ||
| Due to: | Moon orbits Earth in same direction as Earth rotates on its axis. |
b) Sun's gravity also plays a role:
| > Due to Moon's pull (2/3) and Sun's pull (1/3) | of Tides | ||
| > Greater tides when Earth, Moon and Sun lined up (new or full moon) | |||
Variation of gravity with distance:
| > Greatest tides when Moon closest to Earth at new or full moon |
c) Consequences of the tides
i) Synchronous rotation of the moon (e.g. we see same face of our moon)
| because: | moon's sidereal day | = | sidereal month | |||
| or: | period of moon's rotation | = | period of moon's orbit |
The moon started rotating rapidly
| It's tidal bulge lagged due to internal friction: |

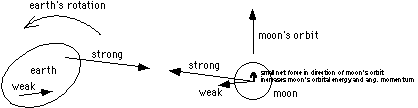
This slowed down the moon's rotation until synchronous rotation was achieved. The process has stopped now. The moon's tidal bulge now points toward the Earth because of its synchronous rotation.
ii) Earth's rotation is gradually slowing down (2/1000 sec/century)
| Cause: | the same process as in (i) now acting on Earth's tidal bulge |
iii) The moon is gradually moving further away from Earth (4cm/year)
| Cause: | Earth's rotation slows down | --> Earth loses angular momentum | |
| --> moon must gain orbital angular momentum | --> moon moves away | ||
C) Precession of the Earth's Axis
Earth tumbles like a spinning top under the moon's gravitational pull
| because: | Earth is not an ideal sphere | ||
| flattened by centrifugal force | |||
| Consequence: | NCP moves around with period of 26,000 years | ||
| -> Vega = polar star in 12,000 years |
Go to